Quite a few times during my work, we often dealt with semantic similarity. Indeed it is a widely used concept which, for example, could be a core functionality for a:
- document management system,
- photo and video cloud product (like Google or Amazon Photo),
- marketing platform which searches similar groups of people using their postings in social media,
- knowledge management system,
- and many other things.
And we’ve learned the hard way some practical specifics essential for Semantic Similarity functionality, which I will share with you today.
Approaches
As usual, we will start with a brief review of the domain.
Most of the time, the algorithm of calculation in Semantic Similarity ML models looks like following:
- Prepare the dataset.
- Train the model of use pre-trained model.
- Encode the texts we would like to compare to be fed to the model.
- Using the model, calculate the similarity of texts or measure how different they are.
The most often and widely used group of approaches are statistical methods based on a corpus. Corpus is a fancy word that means text that you have. Statistical techniques usually work well, but they have certain challenges for practical implementations.
In a nutshell, Corpus-based approaches calculate how often specific words or phrases are used together. For example, the term ‘actor’ is more often used with ‘movie’, but not ‘marshmallow’. This is calculated based on frequencies of certain words (or digrams, trigrams, etc.) that appear in the same phase and/or sentence.
In the same way, an algorithm can calculate the frequencies of specific phrases consisting of two (digram), three (trigram), and more words to appear in the same context (sentence, paragraph, etc.).
Based on statistical analysis (which I explained very briefly, and it is much more complicated), an algorithm can calculate the numerical representation of each word. Words represented by numbers can be combined in a numerical representation of a phrase and/or sentence (and even a paragraph). It is called ‘vector representation’ because we represent a sentence with a vector of numbers which each represents a word (for example, [234, 14, 11, 3, 18].
At first, we ‘tokenize’ the sentence (divide into pieces, and keep only important among them), and then we create a vector representation of a sentence or phrase. Then we feed vector representation to the model, which produces ’embedding’ – a conceptual numerical representation of a word, a sentence, or phrase. To some extent, Embedding represents a concept or a meaning of a word or a sentence.
Embedding is also a vector containing numbers. Depending on how complicated concepts we want to represent, we use different dimensions for a vector. It can be a 16 for something simple or 512 and more dimensions for something more complex.
When we have two embeddings representing sentences, we can calculate their similarity. There are many ways to measure similarities between vectors. It could be Euclidean distance, which measures the distance between all coordinates/values of a vector. Another way of measuring similarity is a Cosine similarity, which works better with NLP because it considers the distance and a cosine between two vectors.
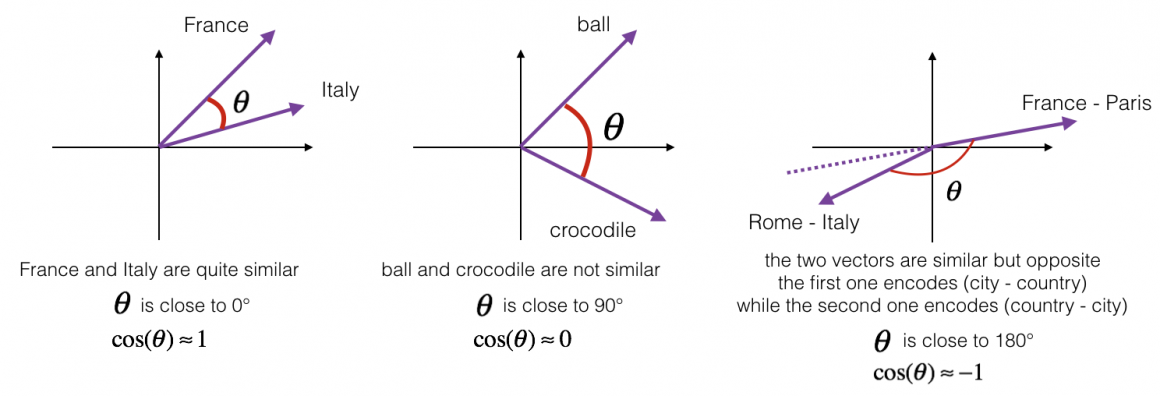
I will not bother you with complicated (and simple formulas) and tell you that there is an easy way to measure Cosine similarity called ‘dot product’. Technically it is not precisely cosine similarity, but it is pretty similar. It measures angle and magnitude between two vectors, while Cosine similarity measures only the angle.
We will review a practical implementation of the dot product below.
Solutions
There are quite a few solutions designed to simplify working with NLP:
- Gensim and NLTK: This combination is the most commonly used toolset in NLP projects. It has everything necessary and a straightforward API.
- Tensorflow: Among other things has a robust set of tools for NLP. Sometimes it is less intuitive than Gensim, for example.
- Google Trax: a reasonably new framework, designed and maintained by Google Brain Team. It has everything necessary to solve complicated NLP challenges. It also has pre-trained Transformers and Reformers, which come in handy when dealing with complex NLP tasks.
- Facebook AI XLM/mBERT and Baidu ERNIE: two relatively new libraries from Facebook and Baidu with a good set of pre-trained Transformer and Reformer models. I was especially impressed by the performance of ERNIE models.
In this article, we will use Gensim + NLTK and Google Trax. I decided to use these due to a few reasons:
- Gensim + NLTK is very popular and will help you accomplish 60% of all NLP tasks.
- Google Trax is a robust framework that uses an optimized calculations module similar to NumPy, which will work well in production-grade pipelines. They call it ‘fast numpy’, and indeed it is speedy.
- These two frameworks will cover 80-90% of all challenges you might face in NLP.
Models
Depending on the tasks at hand, you might want to use:
- a shallow neural net like word2vec containing only two layers,
- deep neural net like BERT, or other Transformer,
to produce appropriate word embeddings.
As well, depending on the deployment limitations and budget, you can:
- either use pre-trained model,
- or train your model.
You can decide to use a pre-trained model. After all, it is the simplest option and requires only a few lines of code to get Embedding. But it also comes with a price. First of all, it was not trained for your specific task, so it will be much bigger than you need. This means it will take more memory and be slower than the one trained for a particular job.
If your task is broad, like, for example, text summarization for corpora without a specific domain, a pre-trained model is a good choice for you. If your task is more specific, it is better to consider training your model.
In this article, we will try both approaches. At first, we will use a pre-trained word2vec shallow neural network. We will use two pre-trained versions ofword2vec:
- ‘glove-wiki-gigaword-100’: model that is about 120+ Mb in size;
- ‘word2vec-google-news-300’: model that is 1600+ Mb in size;
to compare the outcomes.
We will also build and train the Siamese network to compare the performance. It is called Siamese because it consists of two identical networks, producing comparable output vectors. Each network gets one question, and then it creates a vector representing the question. In the end, we calculate the similarity of the two questions.
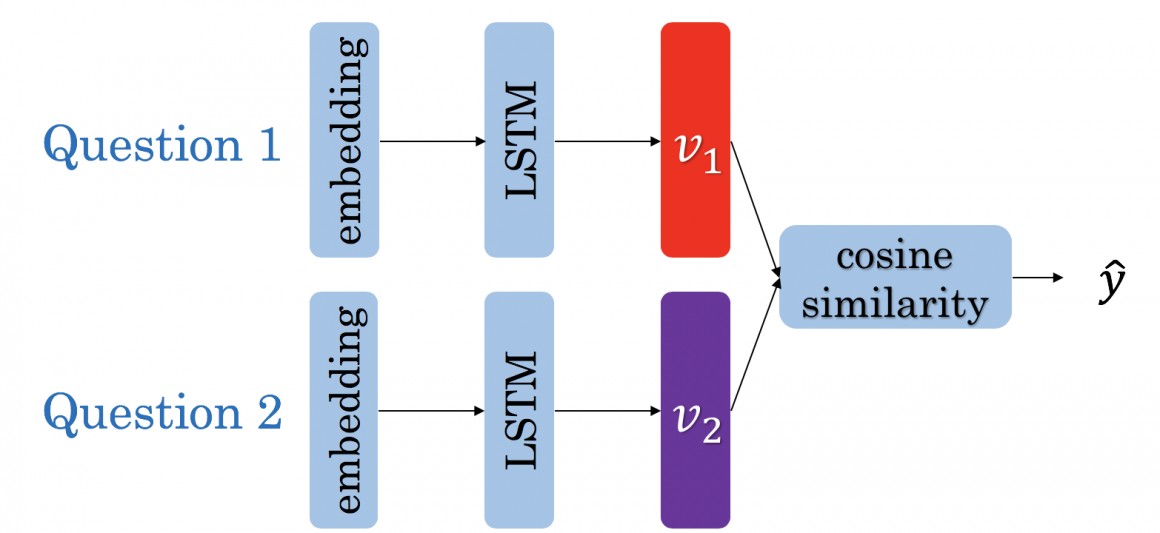
We train this model with a special custom loss function called Triplet Loss (I assume you are familiar with model training and loss functions, so I will not explain these concepts here). This custom loss function ensures that vectors produced by each network are representable. Meaning that if two questions are duplicates, vectors will be such that cosine similarity will be maximum. And if they are not, then cosine similarity will be minimum.
Triplet loss formula might look a bit scary at first, but no worries, I’ll explain how it works:
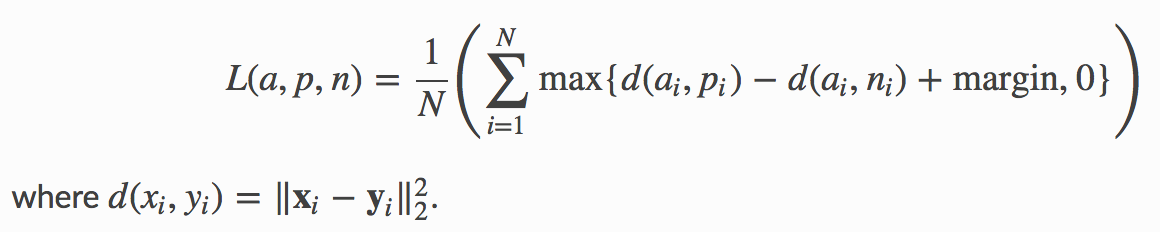
In this formula, ‘a’ represents an ‘anchor’ input which provides zero ground for comparison. We compare anchor with its duplicate input ‘p’ (also called ‘positive’) and non-duplicate ‘n’ (called ‘negative’ input). And we maximize the difference. In simple words, we set a goal for our model to maximize the difference between duplicate and non-duplicate questions, so there is a clear distinguishment.
Pre-trained models
Now let’s take a look at the practical implementation.
As a reminder, we imagine the case where we are building a model for a system that searches similar questions in our knowledge base. It is a part of our chatbot-based support service ecosystem. When a user asks a question, our microservice will find answers provided for a similar question.
For simplification purposes, we will use the following questions to test the performance of our model:
question1 = "How are you?"
question2 = "How are you today?"
question3 = "Are you fine?"
question4 = "Do you enjoy eating the dessert?"
question5 = "Do you like hiking in the desert?"You can see there are two sets of similar questions. One is questions number one, two, and three. And the other one is questions four and five. We want to test if the model will distinguish concepts with different meanings and similar words (4 and 5). We also want our system to understand the difference between similar concepts in questions 1, 2, and 3. We want it to realize that‘How are you today?’ and ‘Are you fine?’ are closer from the standpoint of meaning than ‘How are you today?’ and ‘How are you in general?’. Although from words standpoint situation is quite the opposite.
First of all, we will import the required libraries:
!pip install --upgrade -q gensim
!pip install --upgrade -q annoy
import gensim.downloader as loaderNext, we import the pre-trained model. We will start from a smaller model –glove-wiki-gigaword-100.
word_vectors = loader.load("glove-wiki-gigaword-100")The import should be done within 1 minute, and we can test our pre-trained model. For that purpose, we will use four pairs of questions:
#pair 1
question1 = "How are you?"
question2 = "Are you fine?"
#pair 2
question1 = "Do you enjoy eating the dessert?"
question2 = "Do you like hiking in the desert?"
#pair 3
question1 = "How are you?".lower().split()
question2 = "Do you like hiking in the desert?"
#pair 4
question1 = "How are you?"
question2 = "How are you today?"We will calculate the distance in each pair, like so:
#prepare questions
question1 = "How are you?".lower().split()
question2 = "Are you fine?".lower().split()
#calculate distance
example1 = word_vectors.wmdistance(question1, question2)
print("Example1:", example1, "\n")
#prepare questions
question1 = "Do you enjoy eating the dessert?".lower().split()
question2 = "Do you like hiking in the desert?".lower().split()
#predicting the Duplicated Questions:
example2 = word_vectors.wmdistance(question1, question2)
print("Example2:", example2, "\n")
#prepare questions
question1 = "How are you?".lower().split()
question2 = "Do you like hiking in the desert?".lower().split()
#calculate distance
example3 = word_vectors.wmdistance(question1, question2)
print("Example3:", example3, "\n")
#prepare questions
question1 = "How are you?".lower().split()
question2 = "How are you today?".lower().split()
#calculate distance
example4 = word_vectors.wmdistance(question1, question2)
print("Example4:", example1, "\n")The results we get are following:
Example1: 0.30541094657080253 # "How are you?" vs "Are you fine?"
Example2: 0.4889417319918962 # "Do you enjoy eating the dessert?" vs "Do you like hiking in the desert?"
Example3: 0.7914712506792569 # "How are you?" vs "Do you like hiking in the desert?"
Example4: 0.30541094657080253 # "How are you?" vs "How are you today?"If you are doing the same exercise with me, you should get a similar outcome. The numbers we got represent the distance between two questions. We can see that model thinks that “How are you?” is far away from“Do you like hiking in the desert?” and is closer to “How are you today?” and“Are you fine?”. It is equidistant from bot, which might not exactly be so.
Now we will try to load a model with more parameters trained on a much bigger dataset.
word_vectors = loader.load("word2vec-google-news-300") #1600+ MbAnd run the distance calculations one more time.
#prepare questions
question1 = "How are you?".lower().split()
question2 = "Are you fine?".lower().split()
#calculate distance
example1 = word_vectors.wmdistance(question1, question2)
print("Example1:", example1, "\n")
#prepare questions
question1 = "Do you enjoy eating the dessert?".lower().split()
question2 = "Do you like hiking in the desert?".lower().split()
#predicting the Duplicated Questions:
example2 = word_vectors.wmdistance(question1, question2)
print("Example2:", example2, "\n")
#prepare questions
question1 = "How are you?".lower().split()
question2 = "Do you like hiking in the desert?".lower().split()
#calculate distance
example3 = word_vectors.wmdistance(question1, question2)
print("Example3:", example3, "\n")
#prepare questions
question1 = "How are you?".lower().split()
question2 = "How are you today?".lower().split()
#calculate distance
example4 = word_vectors.wmdistance(question1, question2)
print("Example4:", example1, "\n")The new results would look like the following:
Example1: 0.5710823118871994 # "How are you?" vs "Are you fine?"
Example2: 0.6037490822808392 # "Do you enjoy eating the dessert?" vs "Do you like hiking in the desert?"
Example3: 1.2103087313677972 # "How are you?" vs "Do you like hiking in the desert?"
Example4: 0.5710823118871994 # "How are you?" vs "How are you today?"The numbers above demonstrate pretty much the same proportions as above. And still, our model could not recognize subtle differences, which would be just common sense for humans. The fact that there is a difference between“How are you?” vs“Are you fine?” and“How are you?” (in general) vs“How are you today?”.
This is the end of part 1. Please read part 2 here – Semantic Similarity in Natural language Processing. Part 2.